Regresi merupakan tugas machine learning dalam menemukan hubungan atau pola antara variabel independen (variabel yang diasumsikan mempengaruhi atau menyebabkan perubahan dalam variabel lain) dan variabel dependen (variabel yang nilainya bergantung pada variabel independen) untuk membuat prediksi nilai kontinu (rentang nilai yang tak terbatas). Seperti yang kita ketahui, secara umum tugas machine learning dapat dikategorikan menjadi tiga bagian, yaitu regresi, klasifikasi, dan clustering. Berikut merupakan rinciannya:

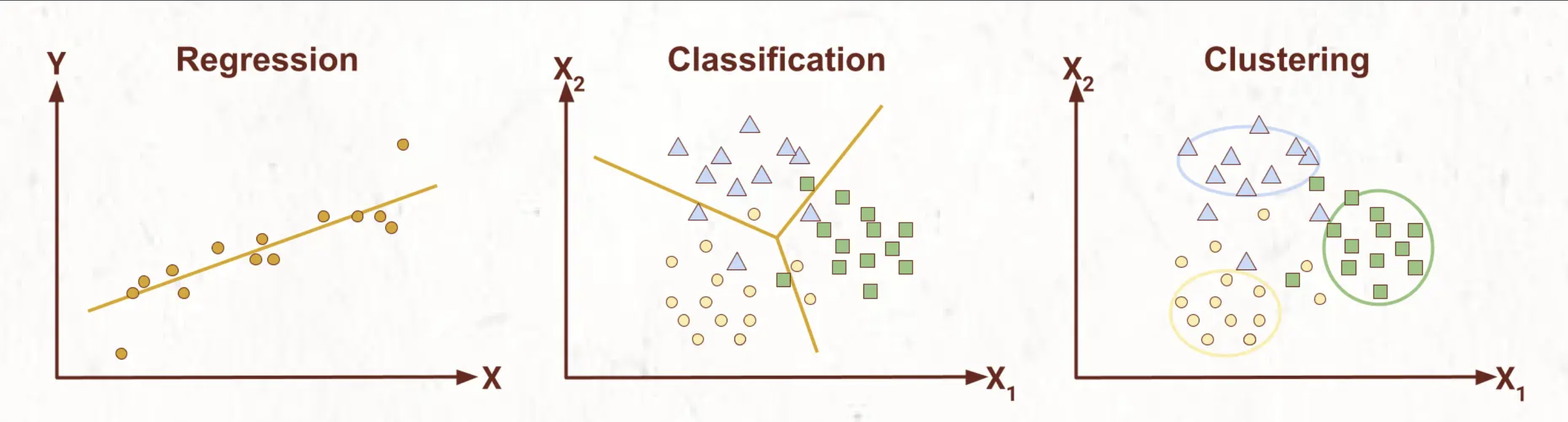
Konsep	Definisi	Algoritma	Kegunaan	Evaluasi
Regresi	Menemukan hubungan atau pola antara variabel independen dan variabel dependen untuk membuat prediksi nilai kontinu.	Linear Regression, Ridge Regression, Lasso Regression, Polynomial Regression, Support Vector Regression (SVR), Prophet, Long Short Term Memory (LSTM), Gated Recurrent Unit (GRU) (GRU)	Prediksi harga rumah berdasarkan fitur-fitur seperti jumlah kamar dan luas tanah. Prediksi CO2 berdasarkan jenis mesin dan tipe mobil.	Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), R-squared (R2).
Klasifikasi	Menyortir atau mengelompokkan data ke dalam kategori atau kelas tertentu berdasarkan fitur-fitur tertentu.	Decision Trees, Random Forest, Support Vector Machines (SVM), K-Nearest Neighbors (KNN)	Identifikasi jenis kelamin berdasarkan fitur-fitur seperti tinggi dan berat. Prediksi gambar binatang berdasarkan anggota tubuh.	Akurasi, presisi, recall, F1-Score, Area Under the ROC Curve (AUC-ROC).
Clustering	Mengelompokkan data ke dalam kelompok atau klaster yang memiliki kemiripan internal.	K-Means Clustering, Hierarchical Clustering (Agglomerative), DBSCAN, Gaussian Mixture Model (GMM)	Segmentasi pelanggan berdasarkan perilaku pembelian. Pengelompokkan teks berdasarkan topik.	Silhouette Score, Davies-Bouldin Index, Calinski-Harabasz Index, Adjusted Rand Index (ARI), Normalized Mutual Information (NMI).

1. Regresi

Definisi: Menemukan hubungan atau pola antara variabel independen dan variabel dependen untuk membuat prediksi nilai kontinu.

Algoritma: Linear Regression, Ridge Regression, Lasso Regression, Polynomial Regression, Support Vector Regression (SVR), Prophet, Long Short Term Memory (LSTM), Gated Recurrent Unit (GRU)

Kegunaan: Prediksi harga rumah berdasarkan fitur-fitur seperti jumlah kamar dan luas tanah.

Evaluasi: Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), R-squared (R2).

2. Klasifikasi

Definisi: Menyortir atau mengelompokkan data ke dalam kategori atau kelas tertentu berdasarkan fitur-fitur tertentu.

Algoritma: Decision Trees, Random Forest, Support Vector Machines (SVM), K-Nearest Neighbors (KNN)

Kegunaan: Identifikasi jenis kelamin berdasarkan fitur-fitur seperti tinggi dan berat.

Evaluasi: Akurasi, presisi, recall, F1-Score, Area Under the ROC Curve (AUC-ROC).

3. Clustering

Definisi: Mengelompokkan data ke dalam kelompok atau klaster yang memiliki kemiripan internal.

Algoritma: K-Means Clustering, Hierarchical Clustering (Agglomerative), DBSCAN, Gaussian Mixture Model (GMM)

Kegunaan: Segmentasi pelanggan berdasarkan perilaku pembelian. Pengelompokkan teks berdasarkan topik.

Evaluasi: Silhouette Score, Davies-Bouldin Index, Calinski-Harabasz Index, Adjusted Rand Index (ARI), Normalized Mutual Information (NMI).

Pada blog ini kita akan menyelami cara kerja beberapa algoritma regresi machine learning, yaitu: Support Vector Regression (SVR), Prophet, Long Short Term Memory (LSTM), Bidirectional Long Short Term Memory (BiLSTM), dan Gated Recurrent Unit (GRU). Metrik evaluasi pada model regresi juga akan dibahas pada blog ini, antara lain: Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), dan R-Squared (R2).

Daftar Isi

Algoritma Regresi
1. Regresi Linear
1.1 Regresi Linear Berganda
1.2 Regresi Linear Polinomial
1.3 Regresi logistik
2. Support Vector Regression (SVR)
3. Prophet
4. Long Short Term Memory (LSTM)
5. Bidirectional LSTM (BiLSTM)
6. Gated Recurrent Unit (GRU)
Metrik Evaluasi
1. Mean Absolute Error (MAE)
2. Mean Squared Error (MSE)
3. Root Mean Squared Error (RMSE)
4. Mean Absolute Percentage Error (MAPE)
5. R-squared (R2)

Algoritma Regresi

Beberapa algoritma dalam tugas regresi antara lain:

1. Regresi Linear

Secara matematis, regresi linear berusaha menemukan lurus terbaik yang mewakili hubungan antara variabel independen (biasanya dilambangkan sebagai X) dan variabel dependen (biasanya dilambangkan sebagai Y). Dalam regresi linear sederhana, persamaan garis regresi linear sederhana dapat ditulis sebagai:

Y=θ_{0}​+θ_{1}​X+ε

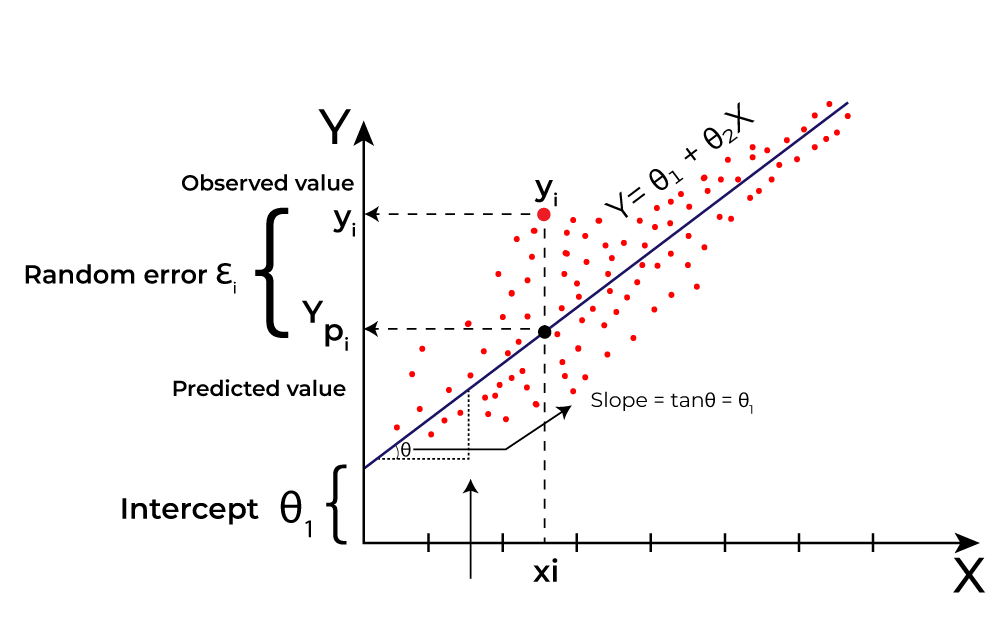
Cara Kerja Regresi Linear (GeeksforGeeks, 2024)

Dimana Y adalah variabel dependen, X adalah variabel independen, θ1 adalah perpotongan dengan sumbu Y (intercept), θ2 adalah koefisien regresi yang mengukur kemiringan garis regresi, dan ε adalah kesalahan acak.

Beberapa regresi liner lainnya, yang sering digunakan yaitu:

1.1 Regresi Linear Berganda

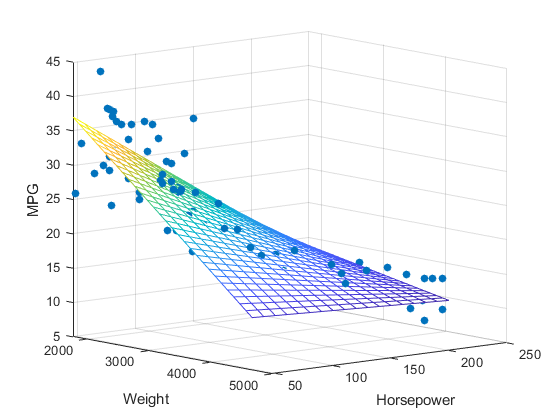
Cara Kerja Regresi Linear Berganda (Kargin, 2021)

Regresi linear berganda melibatkan dua atau lebih variabel independen yang digunakan untuk memprediksi satu variabel dependen. Persamaan regresi linear berganda adalah

Y=θ_{0}​+θ_{1}​X_{1}+​θ_{2}X_{2}+...​+θ_{n}X{n}​+ε

1.2 Regresi Linear Polinomial

Cara Kerja Regresi Linear Polinomial (Herlambang, 2018)

Regresi linear polinomial melibatkan hubungan non-linier antara variabel independen dan variabel dependen. Dalam regresi polinomial, model diperluas dengan memasukkan pangkat variabel independen yang lebih tinggi daripada satu. Contoh persamaan regresi polinomial adalah:

Y=θ_{0}​+θ_{1}​X+​θ_{2}X^{2}​+ε

di mana X^2 menunjukkan hubungan antara X dan Y bukanlah garis lurus.

1.3 Regresi logistik

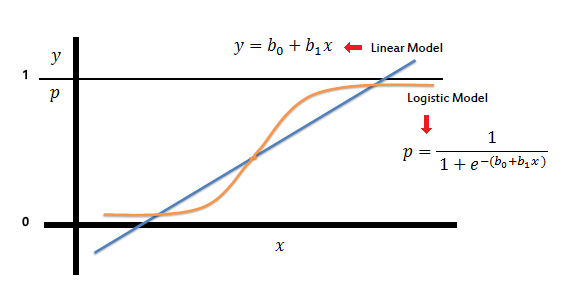
Cara Kerja Logistic Regression (saedsayad.com)

Regresi logistik adalah teknik regresi yang digunakan ketika variabel dependen adalah biner atau kategori, seperti ya/tidak, 0/1, atau kelas-kelas tertentu. Ini merupakan salah satu metode yang paling umum digunakan dalam pemodelan prediksi klasifikasi. Dengan rumus sebagai berikut:

P(Y=1|X) = \frac{1} {1 + e^{-(β_{0} + β_{1}X_{1} + ... + β_{p}X_{p})}}

Fungsi eksponensial ini memastikan bahwa probabilitas yang dihasilkan oleh model selalu berada di antara 0 dan 1.

2. Support Vector Regression (SVR)

Support Vector Regression (SVR) adalah sebuah algoritma machine learning yang digunakan dalam tugas regresi, dengan berfokus pada pencarian garis hyperplane dalam memprediksi nilai target sebaik mungkin. Pada Gambar di bawah ini disajikan gambaran mengenai pengaplikasian algoritma SVR.

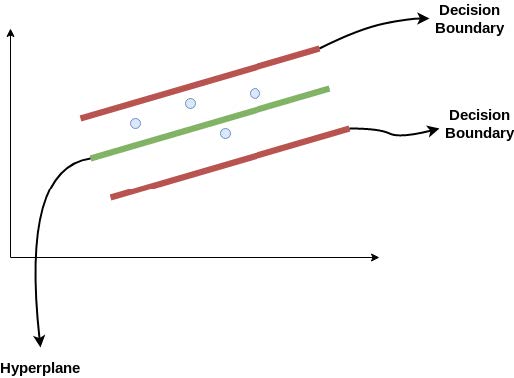
Cara Kerja SVR (Alakh Sethi, 2024)

Jarak antara hyperplane dan decision boundary bisa disebut dengan +a (decision boundary atas) dan -a (decision boundary bawah). Dengan asumsi persamaan dari hyperplane adalah:

Y = 𝑤𝑥 + b

Di mana w adalah bobot yang menentukan arah hyperplane, x adalah vektor input, dan b adalah bias. Maka persamaan decision boundary menjadi:

+𝑎 = 𝑤𝑥+𝑏

−𝑎= 𝑤𝑥+𝑏

Dengan demikian, setiap hyperplane harus memenuhi:

−𝑎<𝑌−𝑤𝑥+𝑏<+𝑎

Sehingga dapat disimpulkan bahwa model SVR berupaya memenuhi kondisi pada rumus di atas, di mana titik-titik yang mendekati hyperplane berada di dalam decision boundary (Trivusi, 2022). Di sisi lain, terdapat dua metode yang dapat dipakai pada algoritma SVR, yaitu metode linear dan non-linear.

Pada metode linear digunakan rumus:

𝑦= Σ(𝑎_{i}−𝑎_{i}^∗)∙<x_{i},𝑥>+ 𝑏

Dimana y adalah output dari model atau prediksi yang ingin kita hasilkan, 𝑎i adalah koefisien dari masing-masing fitur input, ai* adalah koefisien dari masing-masing fitur input pada titik support vektor, xi adalah fitur input, dan b adalah bias yang menentukan posisi hyperplane terhadap titik nol pada sumbu fitur.

Sedangkan pada metode non-linear digunakan rumus:

𝑦= Σ(𝑎_{i}−𝑎_{i}^∗)∙<𝜑(x_{i}),𝜑(𝑥)>+ 𝑏

Dengan y adalah output dari model atau prediksi yang ingin kita hasilkan, 𝑎i koefisien dari masing-masing fitur input 𝜑(𝑥𝑖) yang sudah ditransformasi, 𝑎i* adalah koefisien dari masing-masing fitur input pada titik support vector, ϕ(x) adalah fungsi transformasi (feature mapping) yang mengubah fitur input x menjadi ruang fitur yang berbeda (misalnya, ruang fitur yang memiliki dimensi yang lebih tinggi), dan b adalah bias yang menentukan posisi hyperplane terhadap titik nol pada sumbu fitur.

3. Prophet

Prophet adalah algoritma peramalan waktu untuk mengatasi tantangan peramalan yang kompleks. Algoritma ini dirancang oleh Facebook untuk memodelkan tren musiman harian, mingguan, tahunan, serta memperhitungkan efek hari libur. Secara umum, persamaan yang digunakan pada algoritma prophet adalah:

y(t) = g(t)+s(t)+h(t)+ϵt

Di mana g(t) merupakan fungsi tren yang mewakilkan perubahan nonperiodik dalam time series, s(t) mewakilkan perubahan periodik (seperti musiman harian, mingguan, dan tahunan), dan h(t) mencerminkan pengaruh hari libur. Variabel kesalahan ϵt mewakili perubahan idiosinkratik (faktor-faktor yang bersifat khusus atau unik pada suatu kejadian atau data) yang tidak diakomodasi oleh model (Taylor dan Letham, 2018). Untuk proyeksi tren perubahan nonperiodik g(t) pada prophet, digunakan model pertumbuhan logistik sebagai berikut:

g(t) = \frac{C(t)}{1 + \exp\left(-\left(k + a(t)^T\delta\right)t - \left(m + a(t)^T\gamma\right)\right)}

Model ini menggambarkan pertumbuhan suatu fenomena seiring waktu. Variabel C(t) menggambarkan kapasitas yang bervariasi seiring waktu, k sebagai laju pertumbuhan, a(t) sebagai faktor penyesuaian yang dapat bervariasi seiring waktu, t mewakili titik waktu tertentu, T sebagai titik waktu di mana kita ingin memperkirakan pertumbuhan di masa depan, serta variabel δ, m, dan γ sebagai parameter penyesuaian dalam membentuk kurva pertumbuhan.

Dalam bidang saham ataupun bisnis, seringkali keduanya memiliki perilaku musiman yang berulang pada setiap minggu ataupun tahun. Untuk perubahan periodik s(t) yang melibatkan tren musiman mingguan ataupun tahunan, digunakan rumus Fourier sebagai berikut:

s(t) = \sum\_{n} \left( a_n \cos\left(2\pi n \frac{t}{P}\right) + b_n \sin\left(2\pi n \frac{t}{P}\right) \right)

P merupakan periode reguler yang dari deret waktu (contohnya, P=365,25 untuk data tahunan atau P=7 untuk data mingguan, dalam satuan hari).

Untuk pengaruh hari libur h(t) terhadap suatu fenomena, ditetapkan menggunakan matriks regresor berikut:

Z(t) = [1(t 𝜖 𝐷_{1}),...,1(t 𝜖 𝐷_{𝐿})]

h(t) = Z(t) ⋅ k

Dengan penggunaan k ~ Normal (0, v^2) (Taylor dan Letham, 2018).

4. Long Short Term Memory (LSTM)

Long short term memory (LSTM) merupakan salah satu jenis dari Recurrent Neural Network (RNN) yang mana dilakukan modifikasi terhadap RNN dengan menambahkan memory cell (Masnawi, 2018). Dalam RNN, output dari langkah terakhir diumpankan kembali sebagai input pada langkah yang sedang aktif. Namun, algoritma RNN memiliki kekurangan yaitu tidak dapat memprediksi kata yang disimpan dalam memori jangka panjang (Trivusi, 2022). Arsitektur dari LSTM direpresentasikan di bawah.

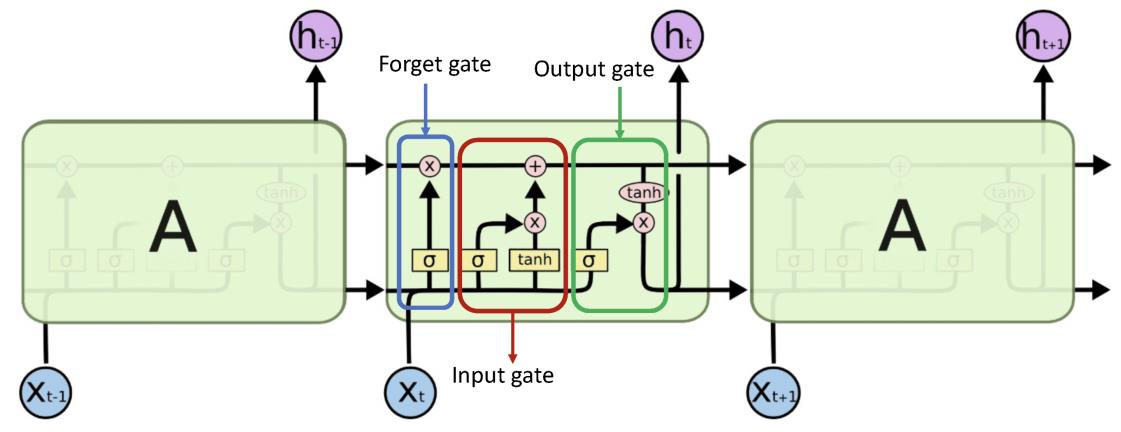
Arsitektur LSTM (Syed & Ahmed, 2023)

Dalam sebuah cell LSTM, terdiri dari forget gate, input gate, dan output gate. Pertama, forget gate adalah pintu yang berfungsi untuk menghapus informasi yang tidak lagi digunakan lagi pada cell dengan mengevaluasi nilai input x[t] dan output s[t-1]. Selanjutnya, input gate merupakan pintu yang berfungsi menampung informasi berguna ke cell state dengan cara menggunakan fungsi sigmoid dan menyaring nilai yang akan disimpan. Terakhir, output gate yang berfungsi untuk mengekstraksi informasi yang berguna dari cell state saat ini untuk disajikan sebagai nilai keluaran (Trivusi, 2022).

5. Bidirectional LSTM (BiLSTM)

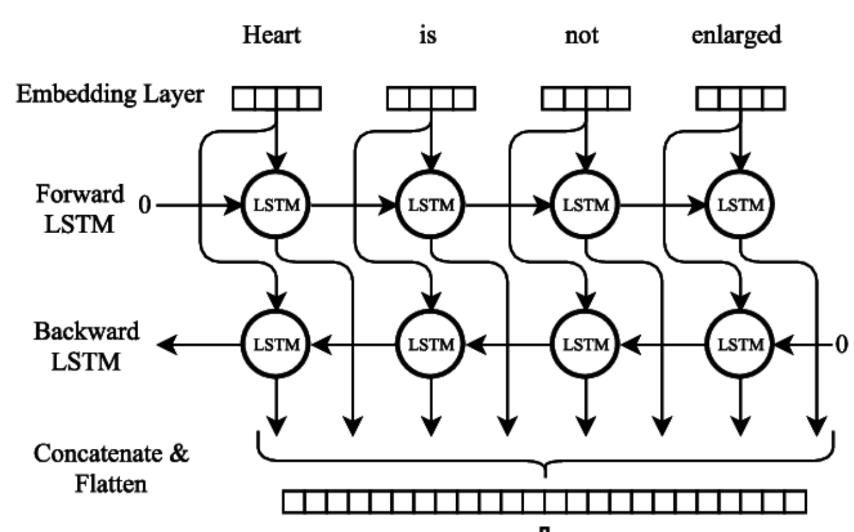
Arsitektur BiLSTM (Cornegruta et al., 2016)

Di sisi lain, BiLSTM adalah perluasan dari model LSTM, di mana dua layer LSTM diterapkan pada data input (Siami-Namini et al., 2019). Arsitektur model BiLSTM dapat dilihat pada Gambar di atas. Kedua layer BiLSTM terdiri atas layer forward dan layer backward yang dapat melakukan pemrosesan dari masa lalu ke masa depan, ataupun sebaliknya tergantung pada kebutuhan spesifik tugas ataupun model.

6. Gated Recurrent Unit (GRU)

Arsitektur GRU (Xin Wang et al., 2019)

Jaringan saraf GRU adalah variasi dari model LSTM dengan mengoptimalkan struktur LSTM dan menggabungkan tiga unit state menjadi dua unit state. Dua state GRU terdiri atas update gate dan reset gate (Xin Wang et al., 2019). Gambar di bawah ini merupakan representasi arsitektur dari GRU.

Model GRU terdiri atas layer input, layer output, dan hidden layer, di mana pada hidden layer terdiri dari neuron GRU. Pada model GRU, diformulasikan rumus sebagai berikut:

r_t = \sigma(W_r^* [h_{t-1}, x_t])

z_t = \sigma(W_z^* [h_{t-1}, x_t])

n_t = \tanh(W^* [r_t^* h_{t-1}, x_t])

h_t = (1 - z_t) \cdot h_{t-1} + z_t \cdot n_t

y_t = \sigma(W_o^* h_t)

Simbol 𝑟𝑡 mencerminkan output dari reset gate pada waktu t, 𝑊𝑟 adalah matriks bobot untuk reset gate, [ℎ𝑡−1,𝑥𝑡] adalah penggabungan dari keadaan tersembunyi sebelumnya ℎ𝑡−1 dan input pada waktu t, 𝑍𝑡 adalah output dari update gate, 𝑊𝑧 adalah matriks bobot untuk update gate, 𝑛𝑡 adalah konten memori baru pada waktu t, W adalah matriks bobot, [𝑟𝑡∗ℎ𝑡−1,𝑥𝑡] adalah penggabungan dari perkalian elemen-wise dari reset gate dan keadaan tersembunyi sebelumnya dengan input pada waktu t, ℎ𝑡 adalah keadaan tersembunyi yang diperbarui pada waktu t, 𝑦𝑡 adalah keluaran pada waktu t, dan 𝑊𝑜 adalah matriks bobot untuk keluaran.

Metrik Evaluasi

Beberapa metrik evaluasi model dalam tugas regresi antara lain:

Catatan: Variabel n adalah jumlah sampel pada data, 𝑦𝑖 merupakan nilai aktual, dan ŷ𝑖 merupakan nilai prediksi.

1. Mean Absolute Error (MAE)

MAE dihitung sebagai rata-rata selisih absolut antara nilai prediksi dan data historis yang diamati (IBM, 2023). MAE memberikan informasi tentang besarnya kesalahan prediksi tanpa memperhatikan arah kesalahan. Perhitungan yang digunakan pada MAE adalah sebagai berikut:

MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|

MAE lebih tidak sensitif terhadap outlier daripada Mean Squared Error (MSE) atau Root Mean Squared Error (RMSE). Jika dataset kita rentan terhadap outlier yang signifikan, menggunakan MAE akan memberikan evaluasi yang lebih stabil.

Selain itu MAE memberikan hasil yang lebih mudah diinterpretasikan, karena hasilnya langsung dalam unit yang sama dengan variabel yang diprediksi. Ini membuatnya lebih mudah dipahami oleh pemangku kepentingan yang tidak memiliki latar belakang matematika atau statistik yang kuat.

2. Mean Squared Error (MSE)

MSE adalah rata-rata dari kuadrat selisih antara nilai prediksi dan nilai sebenarnya. Hal ini memberikan informasi tentang besarnya kesalahan prediksi, dengan memberikan bobot lebih pada kesalahan yang lebih besar. Perhitungan MSE dilakukan dengan menggunakan rumus berikut:

MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2

Jika kita ingin memberikan penekanan lebih pada kesalahan yang besar dalam prediksi, MSE adalah pilihan yang lebih baik. Karena MSE memberikan bobot yang lebih besar pada kesalahan yang lebih besar (dalam bentuk kuadrat), ini berarti model akan lebih sensitif terhadap prediksi yang jauh dari nilai sebenarnya.

3. Root Mean Squared Error (RMSE)

RMSE adalah akar kuadrat dari MSE. Hal ini memberikan nilai kesalahan yang lebih intuitif karena diukur dalam unit yang sama dengan variabel yang diprediksi. Perhitungan RMSE dilakukan dengan menggunakan rumus berikut:

RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}

Apa maksudnya lebih intuitif? Sebagai contoh, jika kita sedang memprediksi harga rumah dalam dolar, maka nilai MSE akan diukur dalam dolar kuadrat (dolar^2). Ini mungkin sulit untuk dipahami secara intuitif, karena unitnya tidak lagi dalam dolar, tetapi dalam dolar yang telah dikuadratkan. Namun, RMSE mengambil akar kuadrat dari MSE, sehingga mengembalikan satuan asli, yaitu dolar. Oleh karena itu, RMSE memberikan nilai kesalahan yang lebih mudah dipahami karena diukur dalam unit yang sama dengan variabel yang diprediksi, dalam contoh ini adalah dolar.

Jadi, ketika kita mengatakan bahwa RMSE memberikan nilai kesalahan yang lebih intuitif, itu berarti bahwa nilai kesalahan tersebut lebih mudah dipahami atau lebih mudah diinterpretasikan dalam konteks masalah yang sedang dipelajari.

Namun, di sisi lain RMSE sangat sensitif terhadap outlier, karena kesalahan dikuadrat sebelum dihitung akar kuadratnya. Jika terdapat outlier yang signifikan dalam data, RMSE bisa menjadi sangat besar, bahkan jika mayoritas prediksi model cukup baik. Dalam kasus ini, metrik alternatif seperti Mean Absolute Error (MAE) mungkin lebih cocok, karena MAE tidak terlalu dipengaruhi oleh outlier.

4. Mean Absolute Percentage Error (MAPE)

MAPE adalah rata-rata selisih persentase absolut antara nilai prediksi dan nilai data yang diamati (IBM, 2023). MAPE berguna untuk memahami sejauh mana kesalahan relatif terhadap besaran sebenarnya. Berikut ini merupakan rumus perhitungan MAPE:

MAPE = \frac{1}{n} \sum_{i=1}^{n} \left| \frac{y_i - \hat{y}_i}{y_i} \right| \times 100\%

Dalam kasus prediksi harga saham yang pernah saya lakukan, harga saham dapat bervariasi dari beberapa dolar hingga ratusan atau bahkan ribuan dolar. Karena Root Mean Squared Error (RMSE) mengukur kesalahan dalam unit yang sama dengan variabel yang diprediksi, nilai RMSE dapat menjadi tidak intuitif untuk diinterpretasikan ketika kita berurusan dengan data yang memiliki rentang nilai yang sangat luas seperti ini.

Dalam kasus seperti itu, lebih disarankan untuk menggunakan metrik evaluasi lain yang lebih sesuai, seperti MAPE. MAPE mengukur kesalahan relatif sebagai persentase dari nilai sebenarnya, sehingga memberikan gambaran yang lebih baik tentang seberapa akurat prediksi kita relatif terhadap rentang nilai saham yang berbeda-beda.

5. R-squared (R2)

R-squared adalah proporsi dari variasi dalam variabel respons yang dapat dijelaskan oleh model regresi. Nilai R2 berkisar antara 0 hingga 1, di mana 1 menunjukkan model yang sempurna cocok dengan data

R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}

R2 dapat digunakan sebagai salah satu kriteria untuk memvalidasi model regresi. Semakin tinggi nilai R2, semakin baik model cocok dengan data dan semakin valid model tersebut.

Dalam penggunaannya, R2 sebaiknya digunakan bersama dengan metrik evaluasi lainnya seperti Mean Squared Error (MSE) atau Mean Absolute Error (MAE) untuk mendapatkan pemahaman yang lebih lengkap tentang kinerja model regresi.